오늘은 데이터 자료구조의 그래프를 알아보자 이말이야.
Graph
그래프는 데이터 자료구조 종류 중 하나이다.
그러면 그래프는 어떻게 자료를 정리할까? 그림을 살펴보자.
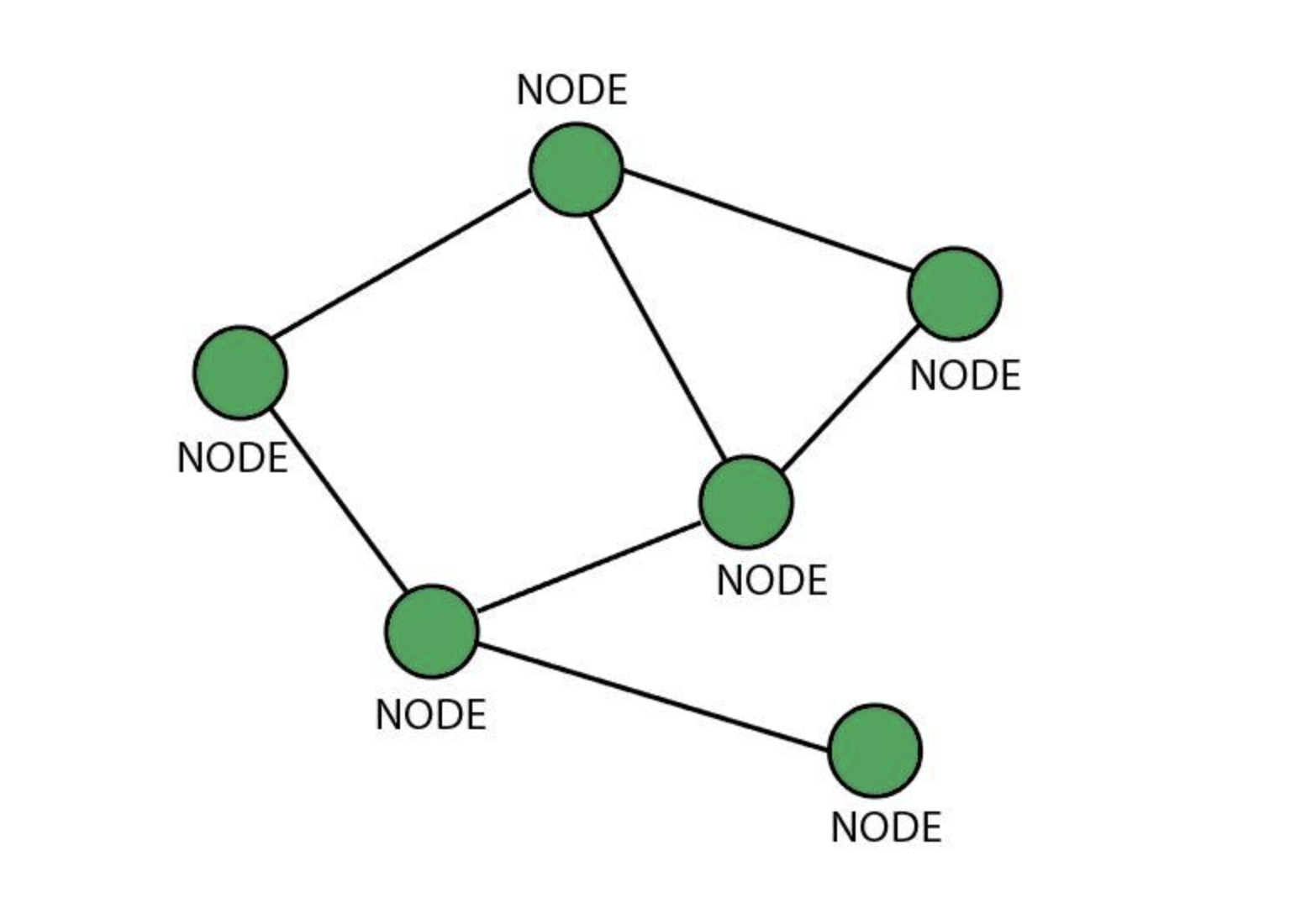
그래프는 위 사진처럼 각 노드(데이터)들을 연결해 주는 선(Edge)가 있다.
요런 자료는 실생활에서 어디서 쓰냐?
지하철 노선도나, 네비게이션이 길을 알려줄 때 쓴다.
각 데이터들은 연결된 edge로 최단 경로나 최소 환승 등을 알려준다고 한다.
Graph 특징들
Graph 구성
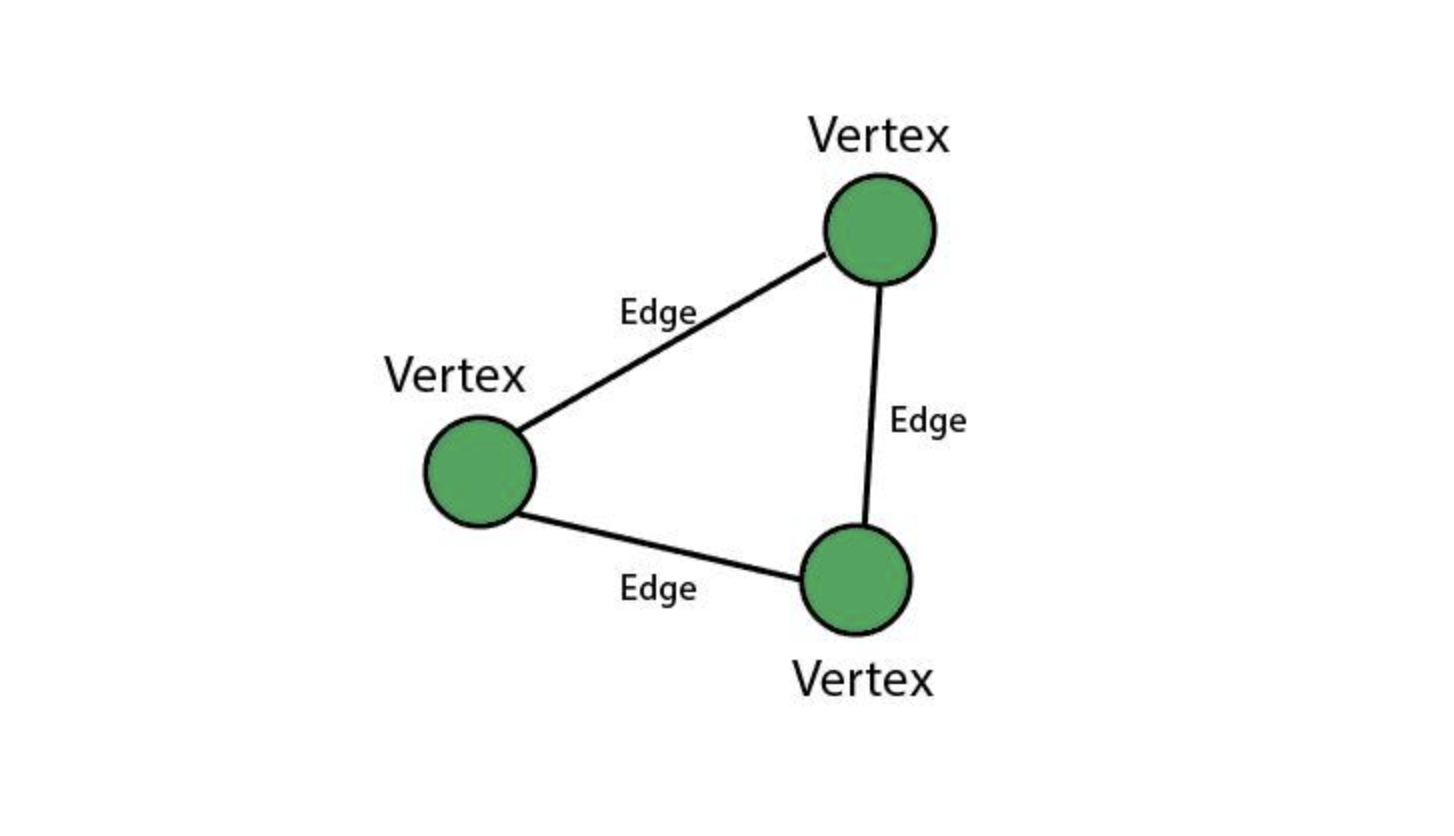
1. Vertex(Node) - 혹은 정점이라고도 한다.
2. Edge - 간선이라고도 한다. vertex와 vertex를 이어주는 선이 있다.
Undirected-무방향 그래프 / directed -방향 그래프
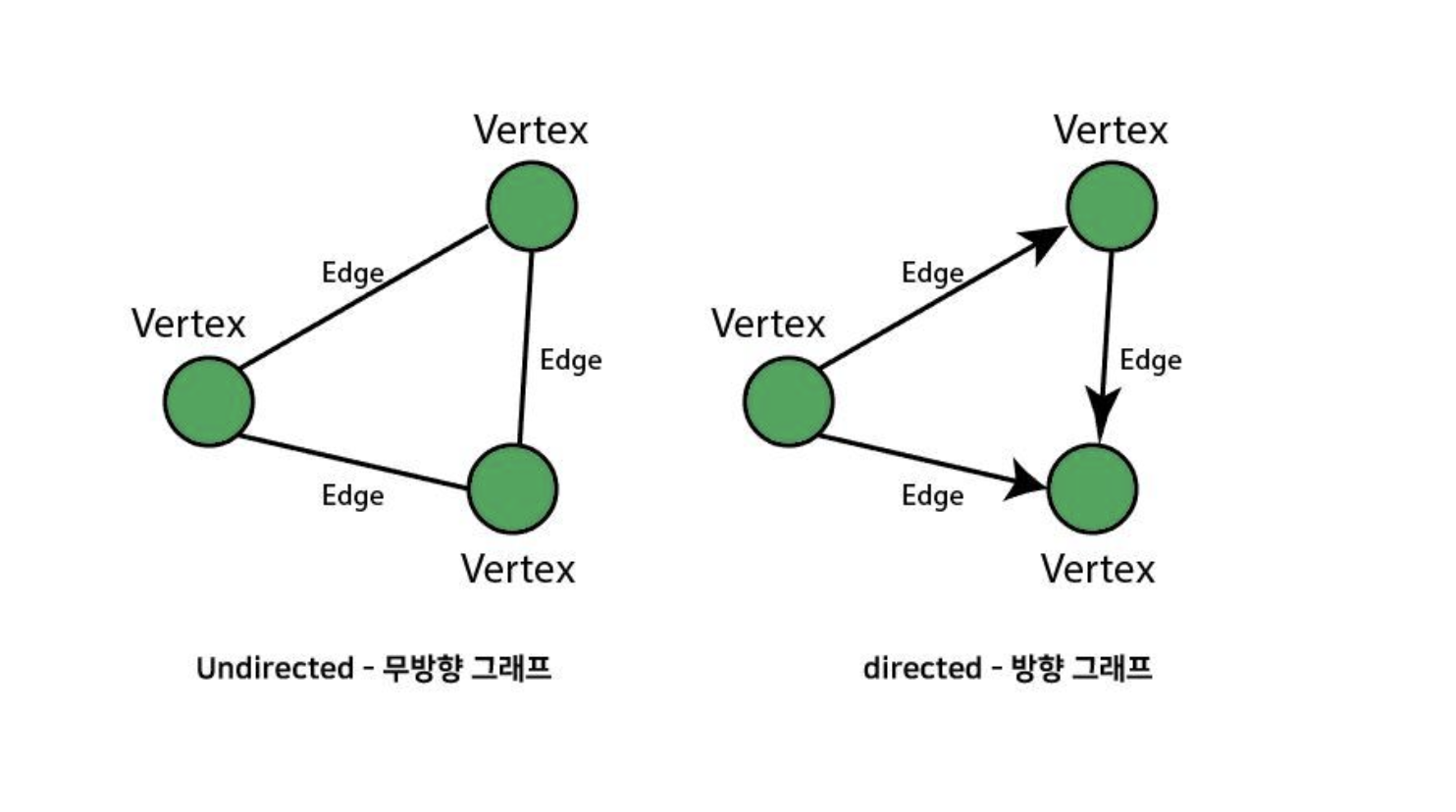
그래프는 2가지로 나뉜다. Undirected-무방향 그래프 / directed -방향 그래프
1. Undirected-무방향 그래프
왼쪽 사진처럼 Edge에 방향 표시가 없는 것이 무방향 그래프다.
무방향 그래프는 Edge로 이어진 Vertex간의 이동이 자유롭다.
내가 밑에서 구현할 코드는 무방향 그래프이다.
2. directed -방향 그래프
오른쪽 사진처럼 방향 표시가 있는 것이 방향 그래프.
당연 편도로만 이동이 가능하다.
Graph의 Cycle
그래프는 자기가 만드는 그래프에 따라 Cycle(출발한 곳에서 나가 다시 돌아올 수 있는 구조)를 만들 수 있고, 심지어 self loof도 가능하다.
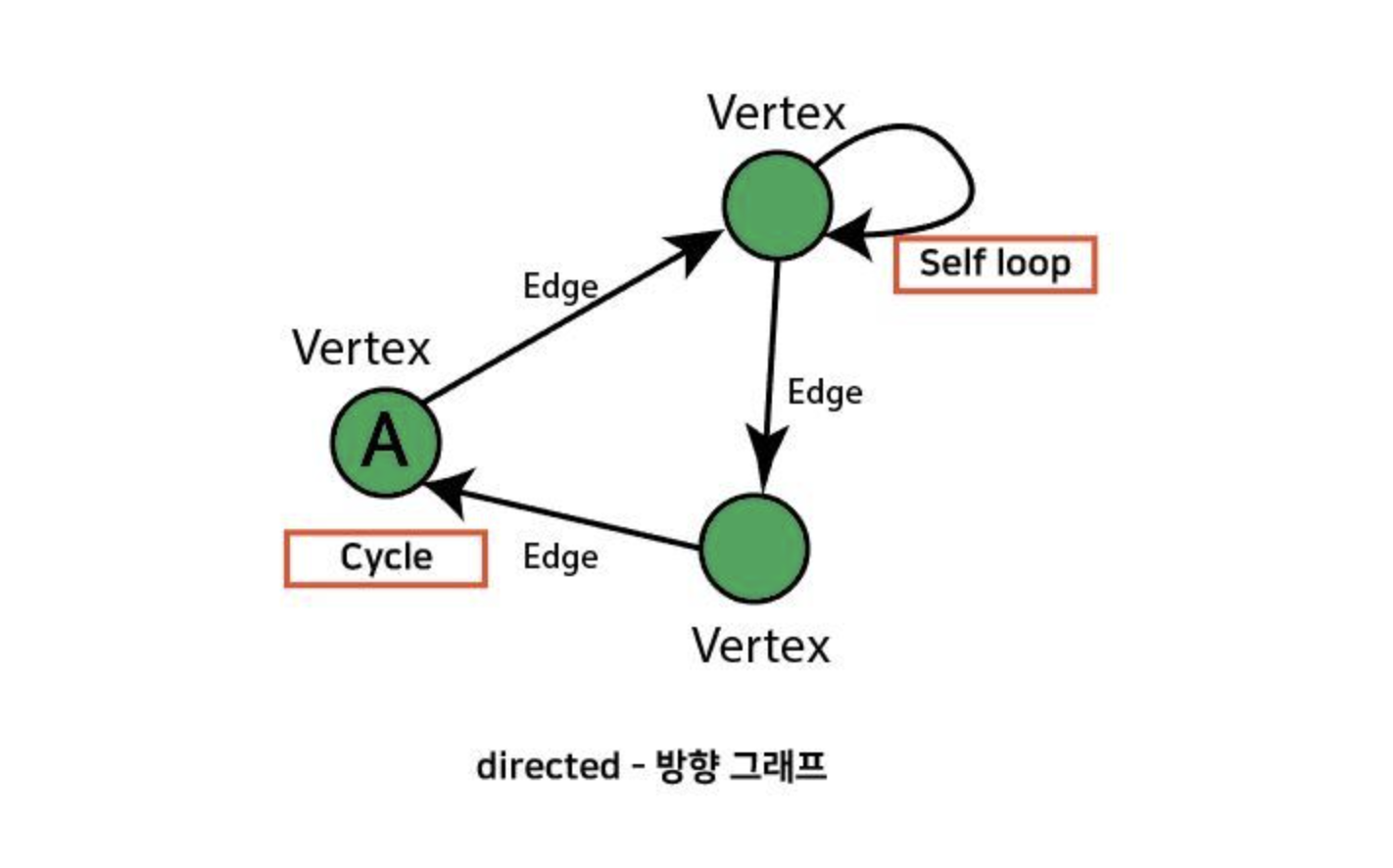
일러스트로 30초 뚝딱하면 만들 수 잇는 사진. 하지만 데스크탑을 왔다 갔다 해야 해서 매우 불편하다.
A의 Edge를 잘 보면 집을 나갔다가 다른 vertex를 들리고 다시 집으로 돌아오는 구조를 볼 수 있다. 이런 모양이 Cycle.
오른쪽 위와 같이 self loof 구조도 있다.
Graph의 degree
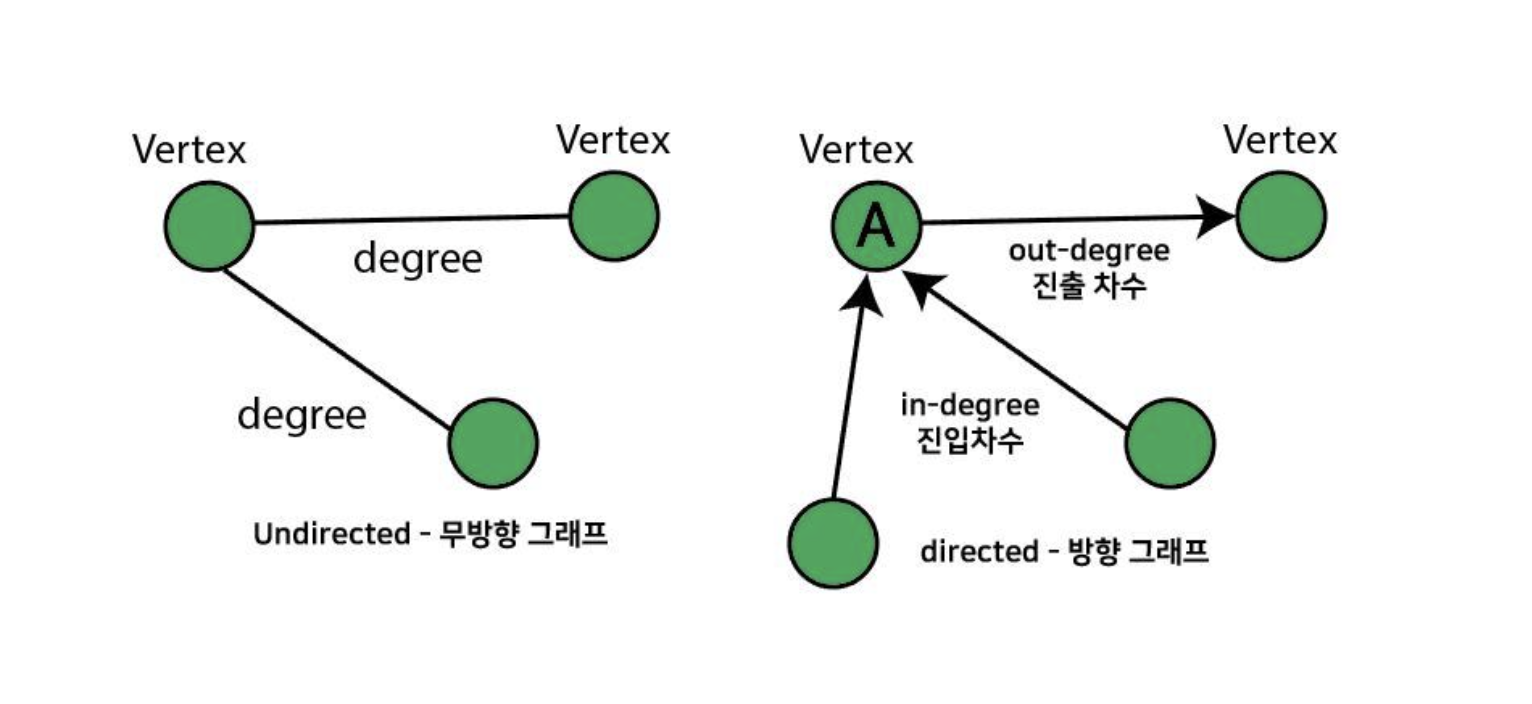
Graph에는 degree가 존재한다.
왼쪽 사진
무방향 그래프에서 하나의 정점에 인접한 정점의 수를 말한다.
제일 왼쪽 Vertex는 2개의 degree를 가지고 있는 것.
오른쪽 사진
방향 그래프에서는
in-degree 방향 그래프에서 외부에서 오는 간선의 수
out-degree 방향 그래픙에서 외부로 향하는 간선의 수
vertex A는 in이 2개, out이 1개인 것.
Graph의 가중치
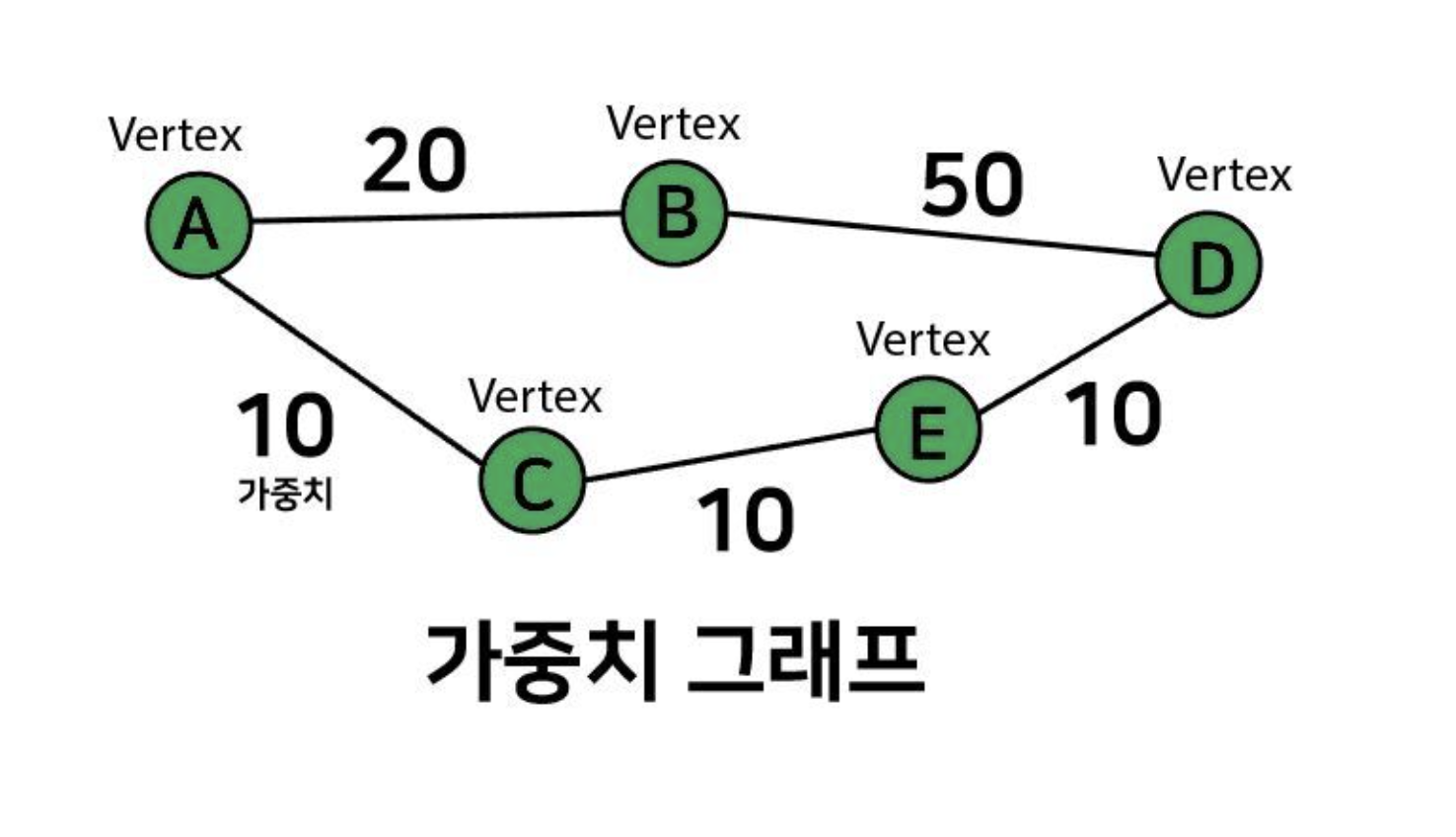
가중치 그래프(Weighted Graph)
간선에 비용이나 가중치가 할당된 그래프
경로를 탐색할 때 들여지는 시간이나 비용 등을 나타낼 수 있따.
만약 A에서 D로 가고 싶으면 A-B-D는 가중치가 총 70이지만
A-C-E-D는 총 가중치가 30이니까, 만약 최소 비용으로 D를 가고 싶다면
요 루트로 가자.
Graph의 2가지 구현 방법
인접 행렬(Adjacency Matrix) 방식
인접 행렬은 그래프의 연결 관계를 이차원 배열로 나타내는 방식이다.
0과 1을 이용한 정수 행렬로 표현할 수 있다.
obj[i][j] : 노드 i에서 노드 j로 가는 간선이 있으면 1, 아니면 0
항상 n^2라는 공간 복잡도가 존재한다.
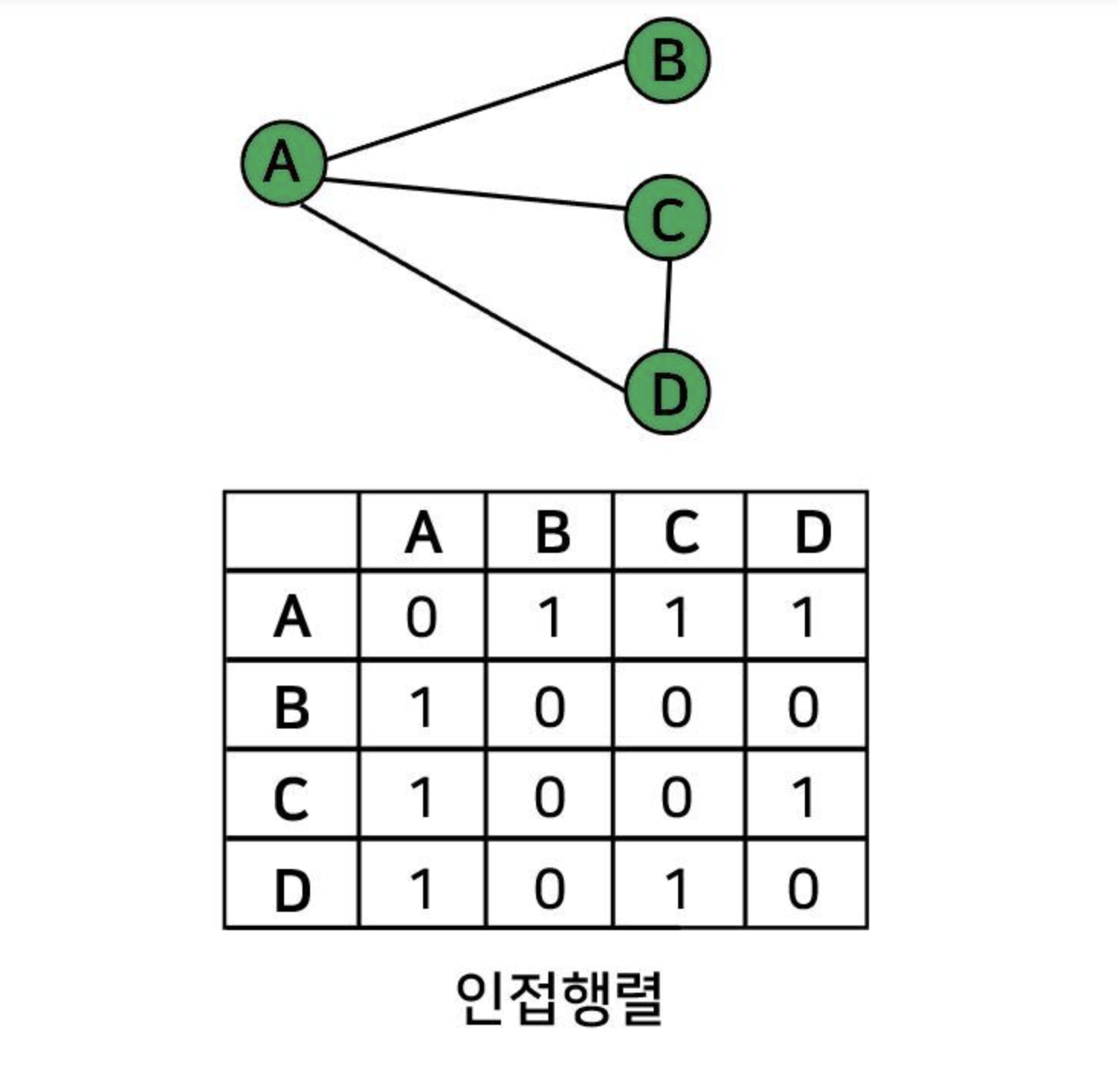
장점 :
구현이 쉽다.
단순 노드끼리의 연결을 확인하고 싶을 때는 O(N)이라는 시간 복잡도 안에서 해결 된다.
간선의 추가와 삭제가 빈번히 일어나는 경우에는 이 방식이 효율적이다.
단점 :
‘a’라는 노드에 연결된 모든 노드를 찾을 때는 총 O(V)의 시간이 걸린다는 점
간선의 수와 무관하게 항상 n^2개의 메모리 공간이 필요하다.
정점의 추가 삭제에는 효율적이지 않다.
인접 리스트(Adjacency List) 방식
가장 일반적인 방식이라고 한다.
linked list랑 비슷하다.
그래프에 존재하는 최대 간선의 수는 O(n+e)이다.
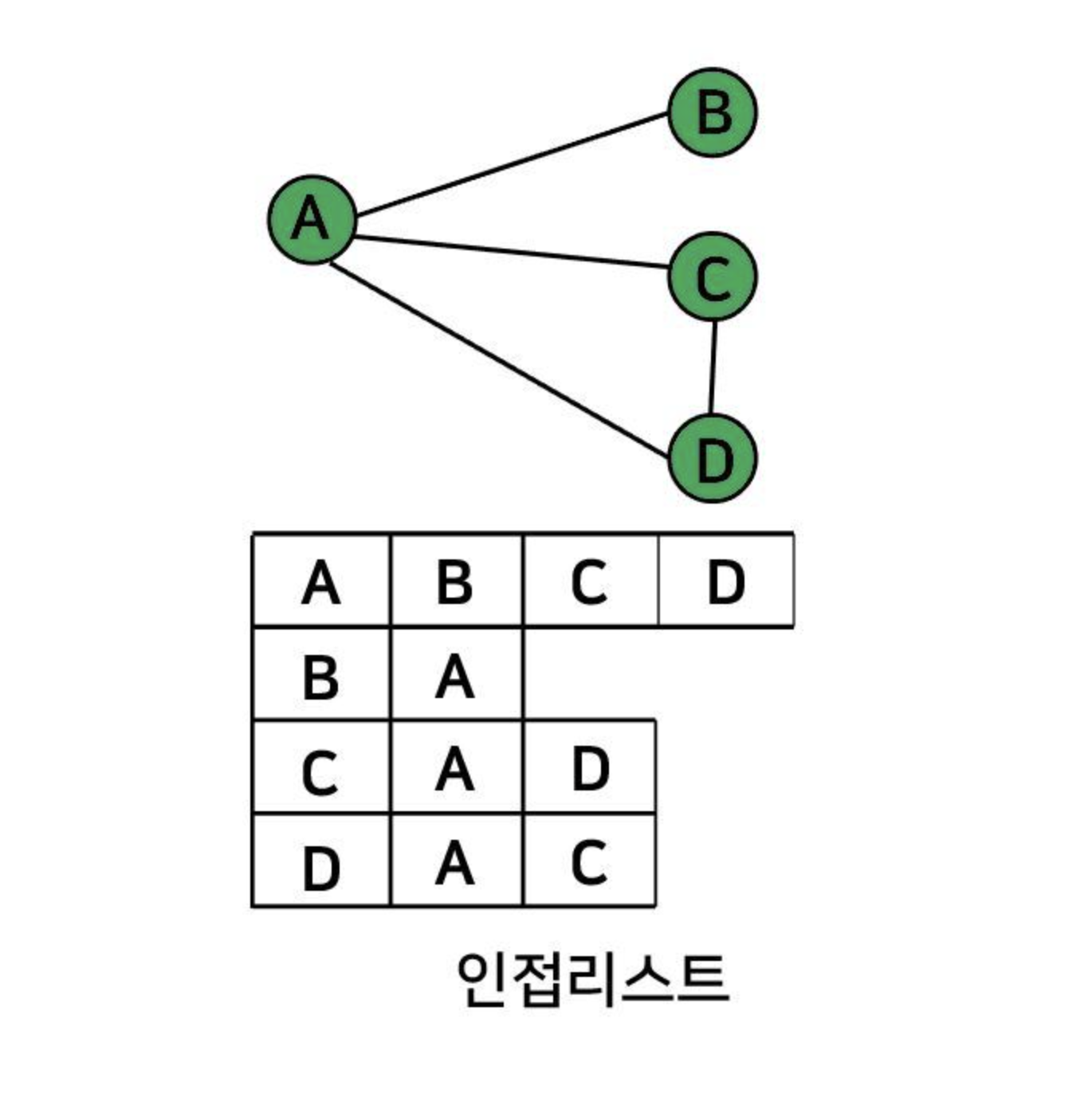
장점 :
vertex의 번호만 알게 된다면 이 번호를 배열의 인덱스로 해서, 각 vertex의 리스트에 쉽게 접근할 수 있다.
정점의 추가 삭제가 빈번히 일어나는 경우에는 이 방식이 효율적이다.
단점:
a가 b와 연결되어 있는 것을 확인하려면 a의 리스트를 순회해야지 b와 연결되어 있는지 확인이 가능하다.
이 경우, O(v)의 시간 복잡도를 갖는다.
반면 인접 행렬이라면, [a][b]가 1인지 0인지만 확인하면 가능하기에 이럴 때 인접행렬은 O(1)만큼만 걸린다.
Graph 메소드
addNode : 그래프에 노드 추가하기
contains: 그래프에 해당 노드가 있는지 확인
removeNode: 노드 삭제하기
hasEdge: 노드와 노드 사이에 엣지가 있는지 확인
addEdge: 노드와 노드 사이에 엣지 추가
removeEdge: 노드와 노드 사이의 엣지 삭제
Graph 코드
배열로 구현할 예정이다. 그리고 무방향 그래프이다.
1. 기본 뼈대
1
2
3
4
5
6
7
8
9
10
11
12
class Graph {
constructor() {
/*
* ex)
* nodes = {
* 0: [ 1, 2 ],
* 1: [ 0 ],
* 2: [ 0 ]
* }
*/
this.nodes = {};
}
부트캠프가 만들어 준 뼈대이다. 착하네?
2. addNode
1
2
3
addNode(node) {
this.nodes[node] = this.nodes[node] || []; //배열로 만들 예정.
}
1
2
3
4
5
6
예시로 이렇게 만들었다고 치자
nodes = {
* 0: [ 1, 2 ],
* 1: [ 0 ],
* 2: [ 0 ]
* }
3. contains
1
2
3
4
5
6
7
contains(node) { // 노드가 있는지 확인하자.
if (this.nodes[node]) { // 노드가 있으면
return true; // 뜨루
} else {
return false // 아니면 펄스
}
}
4. removeNode
1
2
3
4
5
6
7
8
9
removeNode(node) { // 노드 지우기.
if (!this.nodes[node]) { // 노드가 없으면 undefined.
return undefined
}
for (let key of this.nodes[node]) { // this.nodes[node] 안은 배열이기 때문에 of를 썼다.
this.removeEdge(node, key) // 거기 안에서 노드 뿐만 아니라, 연결되어 있던 간선(edge)도 삭제해야 한다.
}
delete this.nodes[node]; // 간선을 지웠다면 노드도 지워주자.
}
1
2
3
4
5
6
7
8
9
nodes = {
* 0: [ 1, 2 ],
* 1: [ 0 ],
* 2: [ 0 ]
* }
여기서 1을 삭제하고 싶으면
우선 nodes[1]에 있는 [0]을 먼저 지우자. removeEdge로.
그 이후 nodes[1]는 객체니까 delete로 지우자.
5. hasEdge
1
2
3
4
5
6
7
8
hasEdge(fromNode, toNode) { // 간선이 있나요?
if (this.nodes[fromNode] && // 만약 A가 있고
this.nodes[fromNode].includes(toNode) // A안에 B가 포함되어 있다면 연결되어 있는 것.
) {
return true
}
return false
}
1
2
3
4
5
6
7
8
9
nodes = {
* 0: [ 1, 2 ],
* 1: [ 0 ],
* 2: [ 0 ]
* }
여기서 1의 간선을 확인하고 싶으면
nodes[1]에 0이 있고, nodes[0]에도 1이 있는지 확인하자.
그래야 뜨루!
6. addEdge
1
2
3
4
addEdge(fromNode, toNode) {
this.nodes[fromNode].push(toNode); // 배열로 추가하기 때문에 push를 썼따. 양방향이라서 서로 추가
this.nodes[toNode].push(fromNode);
}
무방향 그래프이니 양쪽 모두 서로를 추가하자.
7. removeEdge
1
2
3
4
removeEdge(fromNode, toNode) {
this.nodes[fromNode].pop(toNode); // 배열로 추가하기 때문에 pop 썼따. 양방향이라서 서로 삭제
this.nodes[toNode].pop(fromNode);
}
무방향 그래프이니 양쪽 모두 서로를 삭제하자.